阻尼比ζ对系统瞬态响应的影响

　　对于二阶系统，可以用解析法求得阻尼比ζ对时域和频域响应性能指标的影响。但对高阶系统，多个极点会改变二阶系统的分析结论。若高阶系统的闭环主导极点是一对共轭复极点，则可以参考二阶系统的分析结论。

　　假设二阶系统的开环传递函数为：

　　如果H（s）＝1，则闭环传递函数为

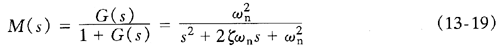
　　式中 ζ——阻尼比；

　　     ω_n——自然（无阻尼）谐振频率。

　　闭环频率响应

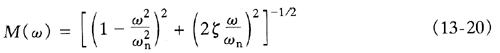
　　谐振频率                                             

　　谐振频率高，意味着阻尼比ζ小，因此上升时间短，响应速度快。

　　谐振峰值

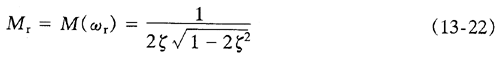
　　ζ＝0，即无阻尼时，Mr→ ∞，ζ＝0.707，Mr＝1即无谐振。

　　因此，谐振峰值Mr也表示系统的相对稳定性。M_r越大，瞬态响应超调量Mp也越大。在0.4＜ζ＜0.7的范围内，1＜M_r＜1.4代表瞬态响应性能较好。当M_r＞1.5时（ζ＜0.4）瞬态响应出现振荡，并出现几次超调。

　　时域中阶跃响应的超调量M_p也与阻尼比ζ有关

　　ζ＝0，即无阻尼时,M_p=1,系统振荡；ζ＝1时，M_p＝0，系统无超调。