单神经元PID控制模块设计思路

　　数控机床的最高运动速度、跟踪精虞、定位精度等重要指标均取决于驱动及位置控制系统的动态与静态性能。因此，研究与开发高性能的驱动系统及位置控制系统，一直是数控机床的关键技术之一．

　　目前数控机床位置伺服控制仍然普遍采用经典控制方法，如比例型或比例2积分型等算法，其优点是算法简便、易于实现，但存在着控制参数适应性差、抗干扰能力不强等缺陷。

　　本模块利用神经网络的自学功能，设计一种在线智能型位置控制算法，图1所示为半闭环位置伺服控制系统结构图。

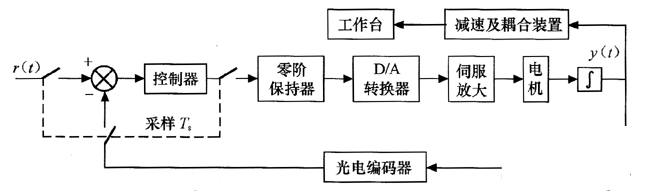
　　图1 半闭环位置伺服控制框图

　　由于丝杠螺距误并以及受载后丝杠 轴承变形等影响，半闭环对检测结果的校正并刁｀完全，控制精度比闭环要低 些，根据自动控制的原理可知，工作台是一个质量元件，传动机构因有变形，可视为弹性元件，两耆构成一个低阻尼振荡环节。半闭环不包含这个环节，一般不会引起进给振荡，而闭环若参数选取不当，则有可能产生不稳定。为了研究问题的方便，可将速度伺服单元等效为一阶惯性环节。

　　式中：K1为速度伺服单元增益（rad／（s·V））；T1为速度伺服单元时间常数，它对应在给定的电压Uand下电机转速θo达到稳态值的63.2％时所对应的时间。通过实验测定，在带载无切削条件下本系统T1≈80ms，而且输出响应基本符合一阶惯性环节。

　　由图1的半闭环位置伺服系统可得如图2所示数控机床位置伺服控制模型。

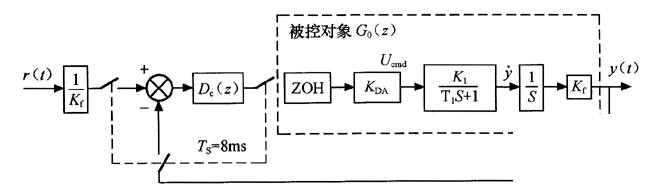
　　图2 数控机床位置伺服单位负反馈框图

　　本模块采用的单神经元控制器原理图如图3所示。

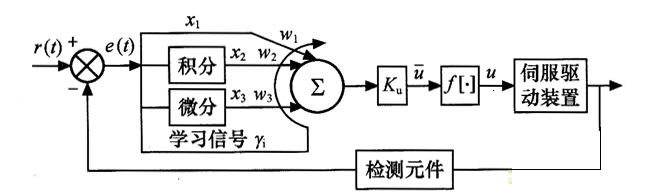
　　图3单神经元控制器

　　本模块提出的学习规则采用反馈原理，同时将Hebb规则与δ规则结合起来，即学习信号取为：

　　图6－x所示的神经元控制率可表示为：

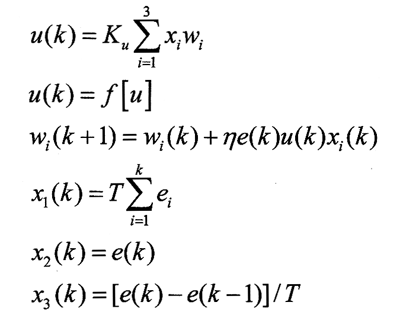
　　式中：Ku为神经元比例系数；f［u］为神经元激发函数。由上面式子可知，这是位置式神经元PID控制器，性能更加优越的增量式PID控制器可表示如下：

　　上式为简单起见，取f［u］＝u.

　　与传统的PID相比，神经元控制仅仅是PID增益，要由学习算法来调整。

　　学习算法是简单的代数运算，因而实时性强。权系数的学习是为了确保系统的跟踪误差收敛于0，只要跟踪误差存在，学习过程就会使权值变化，从而使误差快速趋于0。